Un equipo español de matemáticos y matemáticas, coordinado por Manuel J. Castro y Carlos Parés, del Grupo EDANYA de la Universidad de Málaga (UMA), y Enrique D. Fernández Nieto, de la Universidad de Sevilla (US), en colaboración con investigadores e investigadoras de diferentes universidades y centros de alerta Europa y Estados Unidos, están desarrollado nuevos algoritmos capaces de predecir en tiempo real catástrofes naturales provocadas por temporales marítimos como maremotos, inundaciones o avalanchas.
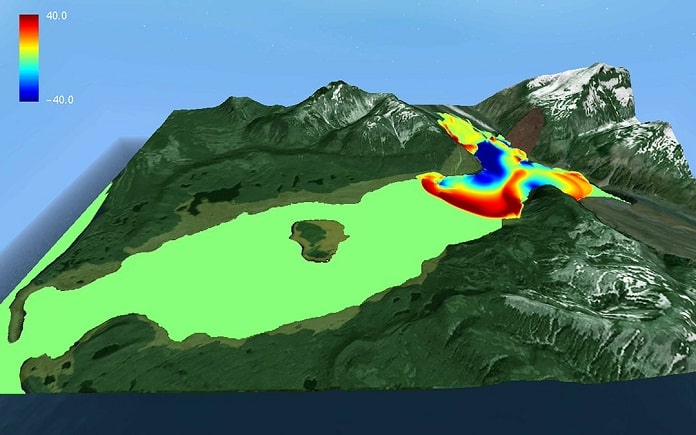
La evolución de las olas de un tsunami o de un deslizamiento submarino puede modelarse mediante un conjunto de ecuaciones matemáticas. Se trata de las ecuaciones en derivadas parciales, que se obtienen de los principios físicos que caracterizan a estos fluidos. En la mayor parte de los casos, resulta imposible obtener soluciones exactas de estas ecuaciones, por lo que es necesario aproximarlas.
El proyecto ‘Leyes de equilibrio no lineales para simulación en mecánica de fluidos: modelización, métodos numéricos, análisis, implementación eficiente y aplicaciones’, está financiado por el Ministerio de Ciencia, Innovación y Universidades (MICIU) a través de la Agencia Estatal de Investigación (AEI) . El equipo investigador propone “innovadores modelos matemáticos” para el estudio y simulación de estos fenómenos. Abordan el diseño y análisis de nuevos algoritmos de aproximación y su implementación eficiente en superordenadores, como los disponibles en el Barcelona Supercomputing Center (BSC) o el CINECA de Italia.
Sólo se dispone de unos minutos para predecir el impacto
“Predecir con precisión y en tiempo real catástrofes naturales como inundaciones o tsunamis es complicado debido a que son fenómenos complejos, no lineales y sujetos a una gran cantidad de datos poco precisos, como, por ejemplo, los datos topo-batimétricos o la dinámica de la ruptura de la falla causante del terremoto”, explica Manuel J. Castro.
“Por otro lado, tsunamis como los de Japón del 2011 son eventos raros y extremos, lo que significa que generalmente no es posible disponer de una serie de datos históricos. Y estos eventos pueden afectar a toda una cuenca oceanográfica, como ocurrió en el Pacífico en 2011, por lo que su simulación requiere un alto esfuerzo computacional. Otras veces son problemas donde se combinan diferentes escalas: sería el ejemplo de la erupción del volcán Hunga Tonga-Hunga Ha'apai en 2022, que generó un maremoto que afectó a la región, pero que también tuvo un efecto global en la atmósfera, generando ondas que se propagaron durante días”.
Relevancia científica y social
Por todo ello, Castro defiende que “el uso de modelos predictivos que puedan dar respuesta en tiempo real plantea diferentes retos desde el punto de vista de las matemáticas, que van desde el diseño y análisis del modelo matemático, su resolución eficiente y robusta, hasta el uso de técnicas de cálculo científico sofisticadas que permitan producir resultados en tiempo real. Además, los modelos deben incorporar la información que se va recopilando al momento con el fin de refinar progresivamente la predicción ofrecida”.
En el equipo investigador consideran que “junto al impacto científico en el campo de las matemáticas y sus aplicaciones, este proyecto tendrá un impacto social relevante: sus resultados llevarán al diseño de nuevas herramientas matemáticas avanzadas que facilitarán el desarrollo de planes de contingencia y la preparación de la población ante amenazas asociadas a desastres naturales, así como la toma de decisiones en tiempo real cuando se producen. Esto será posible mediante la integración de dichas herramientas en distintos sistemas de alerta temprana y plataformas de computación urgente”.